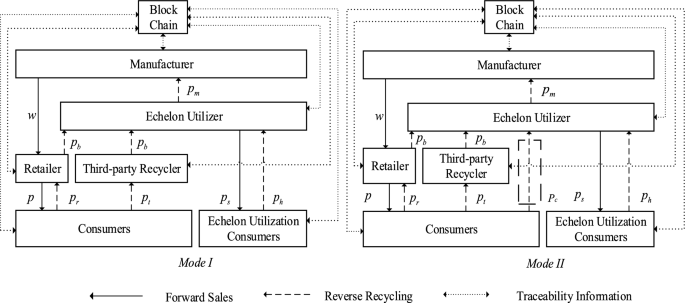
Propositions 1 and 2 provide the optimal decision results for manufacturers, retailers, echelon utilizers, and third-party recyclers under model \(I\) and mode \(II\), respectively. By analyzing the optimal decisions and benefits of the two recycling models, the following inferences can be made.
Corollary 1
The relationship between the manufacturer’s optimal wholesale price, the level of blockchain technology embedding, the retailer’s optimal retail price, and the consumer’s optimal quantity demanded under the two recycling models is shown below:
$$w^{{I^{*} }} = w^{{II^{*} }} ,\;t^{{I^{*} }} = t^{{II^{*} }} ,\;p^{{I^{*} }} = p^{{II^{*} }} ,\;D^{{I^{*} }} = D^{{II^{*} }}$$
Proof
See Online Appendix B.
Corollary 1 demonstrates that the optimal wholesale price, level of blockchain technology embedding, optimal retail price, and optimal quantity demanded by consumers for manufacturers are the same under the two different recycling modes, i.e., the forward supply chain sales decision is not related to the choice of the reverse supply chain recycling mode, and power battery sales and recycling are two relatively independent businesses, and power battery manufacturers are not affected by the recycling mode when making sales decisions.
Corollary 2
In the both recycling modes, the relationship between the variation of manufacturer’s profit with the increase of the residual rate \(\alpha\) of power battery entering the disassembly and utilization stage, the investment cost coefficient \(\mu\) embedded in the blockchain technology, the cost optimization coefficient \(\rho\) of using recycled materials to produce power batteries, and the consumer’s preference \(k\) of traceability information exists as follows: \({{\partial \pi_{m}^{I*} } \mathord{\left/ {\vphantom {{\partial \pi_{m}^{I*} } {\partial \alpha }}} \right. \kern-0pt} {\partial \alpha }} > 0\), \({{\partial \pi_{m}^{II*} } \mathord{\left/ {\vphantom {{\partial \pi_{m}^{II*} } {\partial \alpha }}} \right. \kern-0pt} {\partial \alpha }} > 0\); \({{\partial \pi_{m}^{I*} } \mathord{\left/ {\vphantom {{\partial \pi_{m}^{I*} } {\partial \mu }}} \right. \kern-0pt} {\partial \mu }} < 0\), \({{\partial \pi_{m}^{II*} } \mathord{\left/ {\vphantom {{\partial \pi_{m}^{II*} } {\partial \mu }}} \right. \kern-0pt} {\partial \mu }} < 0\); \({{\partial \pi_{m}^{I*} } \mathord{\left/ {\vphantom {{\partial \pi_{m}^{I*} } {\partial \rho }}} \right. \kern-0pt} {\partial \rho }} < 0\), \({{\partial \pi_{m}^{II*} } \mathord{\left/ {\vphantom {{\partial \pi_{m}^{II*} } {\partial \rho }}} \right. \kern-0pt} {\partial \rho }} < 0\); \({{\partial \pi_{m}^{I*} } \mathord{\left/ {\vphantom {{\partial \pi_{m}^{I*} } {\partial k}}} \right. \kern-0pt} {\partial k}} > 0\), \({{\partial \pi_{m}^{II*} } \mathord{\left/ {\vphantom {{\partial \pi_{m}^{II*} } {\partial k}}} \right. \kern-0pt} {\partial k}} > 0\).
Proof:
See Online Appendix C.
Corollary 2 demonstrates that the profit of the manufacturer increases as the residual rate \(\alpha\) of the power battery entering the dismantling and utilization stage increases in both models. the larger \(\alpha\) indicates that the manufacturer obtains more recycled materials, and since the cost of using recycled materials to produce new power batteries is lower than that of using raw materials34, the more recycled materials that enter the dismantling and utilization stage, the more profit the manufacturer obtains. The profit of manufacturers decreases as the investment cost coefficient \(\mu\) embedded in blockchain technology increases in both models. This is because a higher value of \(\mu\) results in a higher investment cost embedded in the blockchain technology, leading to lower profits for the manufacturer. The manufacturer’s profit decreases in both modes as the cost optimization coefficient \(\rho\) for using recycled materials to produce power batteries increases after blockchain embedding. The manufacturer must evaluate and test recovered non-echelon utilization power batteries to screen out recycled materials for use in producing power batteries. This is necessary because non-echelon utilization power batteries contain waste materials. Therefore, embedding blockchain technology can reduce the cost of using recycled materials to produce power batteries for manufacturers to a certain extent. The cost optimization ability embedded in blockchain technology is expressed by \(1 – \rho\). The larger \(\rho\) is, the higher the cost of using recycled materials \(\rho {\text{c}}_{r}\) to produce power batteries is, and therefore the lower the profit of the manufacturer \(c_{n} – \rho {\text{c}}_{r}\) is. Manufacturers’ profits in both modes increase with the enhancement of consumers’ preference for traceability information \(k\), which stems from the fact that the embedding of blockchain technology under the traceability mechanism can make the gradient of the remaining capacity degradation of SPBs clearly labeled, reduce the information asymmetry in the closed-loop supply chain of the gradient recycling, satisfy the consumers’ preference for traceability information, enhance the consumers’ sense of trust in the transaction, and expand the market breadth for the demand for the gradient utilization, which in turn enhances the manufacturers’ market share and increases the manufacturers’ profits.
Corollary 3
The transfer prices of manufacturers and echelon utilizers for the two recycling models are related as follows:
(1)
\(p_{m}^{{I^{*} }} > p_{m}^{{II^{*} }} ,\;p_{b}^{{I^{*} }} > p_{b}^{{II^{*} }}\);
(2)
When \(2n < m < m_{1}\), if \(F > F_{3}\), then \(p_{r}^{{I^{*} }} = p_{t}^{{I^{*} }} < p_{r}^{{II^{*} }} = p_{t}^{{II^{*} }}\); if \(F_{1} < F < F_{3}\), then \(p_{r}^{{I^{*} }} = p_{t}^{{I^{*} }} > p_{r}^{{II^{*} }} = p_{t}^{{II^{*} }}\);
(3)
When \(m > m_{1}\), if \(F > F_{2}\), then \(p_{r}^{{I^{*} }} = p_{t}^{{I^{*} }} < p_{r}^{{II^{*} }} = p_{t}^{{II^{*} }}\); if \(F_{1} < F < F_{2}\), then \(p_{r}^{{I^{*} }} = p_{t}^{{I^{*} }} > p_{r}^{{II^{*} }} = p_{t}^{{II^{*} }}\);
Proof
See Online Appendix D.
Corollary 3 demonstrates that: (1) the transfer prices of manufacturers and echelon utilizers in Mode \(I\) are higher than in Mode \(II\) due to the diversity of scenarios used by echelon utilizers and the low saturation of battery capacity in Mode \(II\). This results in higher recycling prices than those of retailers and third-party recyclers in Mode \(I\). As a result, consumers are more likely to choose the recycling channels of echelon utilizers, and retailers and third-party recyclers will increase the recycling price to gain access to the recycling market. This will lead to an improvement in the market supply of SPBs in Mode \(II\), which will be higher than in Mode \(I\). In this case, as the market supply increases, the recycling price starts to fall. Consequently, the transfer price will also decrease, leading to an increase in the profit of each recycling participant.
(2) when the recycling channel has a high competitive intensity and the sensitivity of consumers’ recycling is low, if the cost optimization coefficient embedded in the block technology is smaller, i.e., the cost optimization ability is larger, the recycling price of Mode \(I\) is lower than the recycling price of Mode \(II\) If the cost optimization factor is large, meaning that the cost optimization capacity is small, the recovery price Model \(I\) is higher than that of Model \(II\). This is due to the enhanced cost optimization capacity of blockchain technology, which results in higher recycling prices for echelon utilizers compared to that of retailers and third-party recyclers in Mode \(II\). Although the competition sensitivity factor of the recycling channel is larger, due to the smaller recycling price sensitivity factor, the increase of recycling prices by retailers and third-party recyclers will not have a significant impact on the quantity of recycling. Consequently, compared with Mode \(I\), the recycling prices of retailers and third-party recyclers in Mode \(II\) are higher. However, the weaker cost optimization ability does not confer an advantage on echelon utilizers in recycling prices in Mode \(II\). Furthermore, due to the smaller recycling price sensitivity coefficients, retailers and third-party recyclers choose to lower their recycling prices in order to offset the loss of revenues resulting from the reduction in recycling quantities as a consequence of the entry of echelon utilizers into the recycling market.
(3) When the competition in the recycling channel is low and consumers are more sensitive to recycling, the recycling price of Model \(I\) is lower than that of Model \(II\) if the cost optimization coefficient is smaller. Conversely, if the cost optimization coefficient is larger, the recycling price of Model \(I\) is higher than that of Model \(II\). This is because the stronger cost-optimization capability makes the echelon utilizer’s recycling price significantly higher than that of the retailer and third-party recycler in Mode \(II\), and although the competitive sensitivity coefficient of the recycling channel is smaller, the amount of recycling changes significantly when the retailer and third-party recycler increase their recycling price due to the larger recycling price sensitivity coefficient, so the retailer and third-party recycler will increase their recycling price in Mode \(II\) and thus higher than in Model \(I\). When the cost optimization ability is weak, the recycling price of the echelon utilizer in Model \(II\) is not significantly different from that of the retailer and the third-party recycler, and although the recycling price sensitivity coefficient is larger, the retailer and the third-party recycler will choose to lower the recycling price to reduce the profit loss.
Corollary 4
The optimal recycling quantities for third-party recyclers and retailers under the two recycling models have a relationship as follows:
(1)
\(Q_{t}^{{I^{*} }} = Q_{r}^{{I^{*} }} > Q_{t}^{{II^{*} }} = Q_{r}^{{II^{*} }}\);
(2)
When \(1 > \alpha > \alpha_{1}\), \({{\partial (Q_{r}^{{I^{*} }} – Q_{r}^{{II^{*} }} )} \mathord{\left/ {\vphantom {{\partial (Q_{r}^{{I^{*} }} – Q_{r}^{{II^{*} }} )} {\partial \beta }}} \right. \kern-0pt} {\partial \beta }} = {{\partial (Q_{t}^{{I^{*} }} – Q_{t}^{{II^{*} }} )} \mathord{\left/ {\vphantom {{\partial (Q_{t}^{{I^{*} }} – Q_{t}^{{II^{*} }} )} {\partial \beta }}} \right. \kern-0pt} {\partial \beta }} > 0\), when \(0 < \alpha < \alpha_{1}\), \({{\partial (Q_{r}^{{I^{*} }} – Q_{r}^{{II^{*} }} )} \mathord{\left/ {\vphantom {{\partial (Q_{r}^{{I^{*} }} – Q_{r}^{{II^{*} }} )} {\partial \beta }}} \right. \kern-0pt} {\partial \beta }} = {{\partial (Q_{t}^{{I^{*} }} – Q_{t}^{{II^{*} }} )} \mathord{\left/ {\vphantom {{\partial (Q_{t}^{{I^{*} }} – Q_{t}^{{II^{*} }} )} {\partial \beta }}} \right. \kern-0pt} {\partial \beta }} < 0\);
(3)
\({{\partial (Q_{r}^{{I^{*} }} – Q_{r}^{{II^{*} }} )} \mathord{\left/ {\vphantom {{\partial (Q_{r}^{{I^{*} }} – Q_{r}^{{II^{*} }} )} {\partial \rho }}} \right. \kern-0pt} {\partial \rho }} = {{\partial (Q_{t}^{{I^{*} }} – Q_{t}^{{II^{*} }} )} \mathord{\left/ {\vphantom {{\partial (Q_{t}^{{I^{*} }} – Q_{t}^{{II^{*} }} )} {\partial \rho }}} \right. \kern-0pt} {\partial \rho }} < 0\); \({{\partial (Q_{r}^{{I^{*} }} – Q_{r}^{{II^{*} }} )} \mathord{\left/ {\vphantom {{\partial (Q_{r}^{{I^{*} }} – Q_{r}^{{II^{*} }} )} {\partial \varphi }}} \right. \kern-0pt} {\partial \varphi }} = {{\partial (Q_{t}^{{I^{*} }} – Q_{t}^{{II^{*} }} )} \mathord{\left/ {\vphantom {{\partial (Q_{t}^{{I^{*} }} – Q_{t}^{{II^{*} }} )} {\partial \varphi }}} \right. \kern-0pt} {\partial \varphi }} < 0\)
Proof
See Online Appendix E.
Corollary 4 demonstrates that (1)the recycling quantities of retailers and third-party recyclers in Model \(I\) and Model \(II\) of the closed-loop supply chain for the echelon recycling of power batteries embedded in the blockchain under the traceability mechanism are equal when they reach optimal profit. Additionally, the optimal recycling quantities in Model \(I\) are higher than those in Model \(II\) due to the smaller competition intensity of the recycling channel in Model \(I\). (2) When the residual rate \(\alpha\) of the SPBs into the stage of dismantling and utilization is large, the difference between the optimal recycling quantities of retailers and third-party recyclers in Mode \(I\) and Mode \(II\) increases with the increase of the spent power battery’s echelon utilization rate \(\beta\), and conversely, the difference between the optimal recycling quantities decreases with the increase of \(\beta\). This is because when \(\alpha\) is larger, the manufacturer can get more recycled materials to produce power batteries. This is more profitable than using raw materials to produce power batteries, which prompts the manufacturer to produce more power batteries. As a result, the recycling quantity increases. The increase in recycling quantity is greater for Mode \(I\), which has a lower competitive intensity of recycling subjects, than for Mode \(II\). This leads to a greater difference between the recycling quantity of retailers and third-party recyclers in Mode \(I\) and Mode \(II\). On the contrary, when \(\alpha\) is small, manufacturers will produce fewer power batteries, and the number of SPBs recycled will decrease, and the decrease in the number of recycled batteries in Mode \(I\), where the intensity of competition among recycling entities is lower, is greater than that in Mode \(II\). This results in a decrease in the difference in the number of recycled batteries recycled by retailers and third-party recyclers between Mode \(I\) and Mode \(II\). (3) As \(\varphi\) and \(\rho\) increase, the difference in recycling quantity between retailers and third-party recyclers decreases in both Mode \(I\) and Mode \(II\). Increases in \(\varphi\) indicate a weakened ability for cost optimization, resulting in higher costs for laddering utilizers. This prompts a decrease in transfer prices, leading to reduced recycling prices for retailers and third-party recyclers. As a result, the quantity of recycling decreases. Increases in \(\rho\) indicate higher manufacturing costs for power batteries, leading to a decrease in the number of batteries produced and recycled. The decrease in the number of recycled batteries is larger in Mode \(I\) than in Mode \(II\).
Corollary 5
If \(m > m_{2}\), then \(Q^{{I^{*} }} < Q^{{II^{*} }}\); If \(2n < m < m_{2}\) and \(0 < F < F_{4}\), then \(Q^{{I^{*} }} < Q^{{II^{*} }}\); If \(2n < m < m_{2}\) and \(F > F_{4}\), then \(Q^{{I^{*} }} > Q^{{II^{*} }}\).
Proof
See Online Appendix F.
Corollary 5 demonstrates that: (1) When the recycling channel’s competitive intensity is low and the recycling price sensitivity is high, the total recycled quantity of retired power batteries of Model \(I\) is always smaller than that of Model \(II\). This is because, although the sensitivity coefficient of competition in recycling channels is smaller, the sensitivity coefficient of recycling prices is larger, and each recycling participant is more sensitive to price changes, while the participation of echelon utilizers in recycling in Mode \(II\) can offer higher recycling prices, which attracts more SPBs to the recycling market. (2) When the competition among recycling channels is high and the price sensitivity of recycling is low, and at the same time the level of cost optimization coefficient embedded in the blockchain technology is low, the total quantity of retired power batteries recycled for Model \(I\) is smaller than that for Model \(II\). Conversely, when the competition among recycling channels is higher and the price sensitivity of recycling is lower, and at the same time the level of cost optimization coefficient embedded in the blockchain technology is higher, the total quantity of retired batteries recycled for Model \(I\) is greater than that for Model \(II\). This is due to the fact that when the cost optimization factor of blockchain technology is at a low level, both echelon utilizers and manufacturers in the two modes tend to set lower transfer prices and recycling prices, and although the sensitivity coefficient of competition in recycling channels is larger, the lower sensitivity coefficient of recycling price makes the recycling quantity of SPBs in Mode \(II\) higher than that in Mode \(I\). However, if the cost optimization factor of blockchain technology is increased to a higher level, the echelon utilizers and manufacturers in both modes will increase the transfer price and recycling price accordingly, and this change will make the recycling quantity of SPBs in Mode \(II\) lower than that in Mode \(I\). The manufacturer must adjust the cost optimization coefficient based on the competitive intensity of the recycling channel, price sensitivity of recycling, and recycling mode. For instance, if the competition among recycling participants in the recycling channel is intense and consumers are moderately sensitive to the recycling price, the manufacturer should decrease the level of cost optimization coefficient for recycling mode \(II\) and increase it for recycling mode \(I\).
Corollary 6
The profit relationship between the third-party recycler and the retailer under the two recycling models is as follows:
(1)
\(\pi_{r}^{{I^{*} }} > \pi_{r}^{{II^{*} }}\), \(\pi_{t}^{{I^{*} }} > \pi_{t}^{{II^{*} }}\);
(2)
If \(1 > \alpha > \alpha_{1}\), then \({{\partial (\pi_{r}^{{I^{*} }} – \pi_{r}^{{II^{*} }} )} \mathord{\left/ {\vphantom {{\partial (\pi_{r}^{{I^{*} }} – \pi_{r}^{{II^{*} }} )} {\partial \beta }}} \right. \kern-0pt} {\partial \beta }} > 0\), \({{\partial (\pi_{t}^{{I^{*} }} – \pi_{t}^{{II^{*} }} )} \mathord{\left/ {\vphantom {{\partial (\pi_{t}^{{I^{*} }} – \pi_{t}^{{II^{*} }} )} {\partial \beta }}} \right. \kern-0pt} {\partial \beta }} > 0\); If \(0 < \alpha < \alpha_{1}\), \({{\partial (\pi_{r}^{{I^{*} }} – \pi_{r}^{{II^{*} }} )} \mathord{\left/ {\vphantom {{\partial (\pi_{r}^{{I^{*} }} – \pi_{r}^{{II^{*} }} )} {\partial \beta }}} \right. \kern-0pt} {\partial \beta }} < 0\), \({{\partial (\pi_{t}^{{I^{*} }} – \pi_{t}^{{II^{*} }} )} \mathord{\left/ {\vphantom {{\partial (\pi_{t}^{{I^{*} }} – \pi_{t}^{{II^{*} }} )} {\partial \beta }}} \right. \kern-0pt} {\partial \beta }} < 0\);
(3)
\({{\partial (\pi_{r}^{{I^{*} }} – \pi_{r}^{{II^{*} }} )} \mathord{\left/ {\vphantom {{\partial (\pi_{r}^{{I^{*} }} – \pi_{r}^{{II^{*} }} )} {\partial \rho }}} \right. \kern-0pt} {\partial \rho }} < 0\), \({{\partial (\pi_{t}^{{I^{*} }} – \pi_{t}^{{II^{*} }} )} \mathord{\left/ {\vphantom {{\partial (\pi_{t}^{{I^{*} }} – \pi_{t}^{{II^{*} }} )} {\partial \rho }}} \right. \kern-0pt} {\partial \rho }} < 0\), \({{\partial (\pi_{r}^{{I^{*} }} – \pi_{r}^{{II^{*} }} )} \mathord{\left/ {\vphantom {{\partial (\pi_{r}^{{I^{*} }} – \pi_{r}^{{II^{*} }} )} {\partial \varphi }}} \right. \kern-0pt} {\partial \varphi }} < 0\), \({{\partial (\pi_{t}^{{I^{*} }} – \pi_{t}^{{II^{*} }} )} \mathord{\left/ {\vphantom {{\partial (\pi_{t}^{{I^{*} }} – \pi_{t}^{{II^{*} }} )} {\partial \varphi }}} \right. \kern-0pt} {\partial \varphi }} < 0\)
Proof:
See Online Appendix G.
Corollary 6 demonstrates that: (1) Given a recycling market size, both retailers and third-party recyclers in Model \(I\) are more profitable than in Model \(II\). This is due to the higher optimal quantity of recycling in Model \(I\) compared to Model B, as well as the lower intensity of competition in the recycling channel in Model \(I\). (2) The optimal profit difference between retailers and third-party recyclers in Model \(I\) and Model \(II\) increases with \(\beta\) when \(\alpha\) is larger; otherwise, it decreases with \(\beta\). This is because manufacturers can obtain more recycled materials when the residual rate of power batteries entering the dismantling and utilization stage is higher. This is more profitable than using raw materials to produce power batteries, which enhances the manufacturer’s incentive to produce and recycle. As a result, the optimal profit increases successively. Mode \(I\), which has a lower intensity of recycling competition, experiences a larger profit increase than Mode \(II\). On the contrary, if the residual rate of power batteries during the dismantling and utilization stage is low, the manufacturer’s production of power batteries using recycled materials decreases. This leads to a decrease in marginal revenue, recycling incentives, and the number of recycling, resulting in a decrease in the manufacturer’s optimal profit. The decrease in profit is larger in Model \(I\) than in Model \(II\). (3) The difference in optimal profits between retailers and third-party recyclers in Mode \(I\) and Model \(II\) decreases as \(\varphi\) and \(\rho\) increase. This is because an increase in the optimization coefficient of the processing cost of the power battery’s echelon use, \(\varphi\), weakens the ability to optimize the cost and increases the cost of echelon users. This drives the transfer price down, resulting in a decrease in optimal profits for both retailers and third-party recyclers. An increase in the optimization factor \(\rho\) for the processing cost of power batteries using recycled materials results in an increase in the manufacturer’s production cost of power batteries. This, in turn, leads to an increase in the selling and recycling prices of power batteries. As a result, the optimal profit of retailers and third-party recyclers decreases. In Mode \(I\), the decrease in profit is greater than that in Mode \(II\).
Corollary 7
If \(2n < m < m_{2}\) and \(F > F_{6}\), then \(\pi_{c}^{{I^{*} }} > \pi_{c}^{{II^{*} }}\); If \(2n < m < m_{2}\) and \(0 < F < F_{6}\), then \(\pi_{c}^{{I^{*} }} < \pi_{c}^{{II^{*} }}\); If \(m > m_{2}\), then \(\pi_{c}^{{I^{*} }} < \pi_{c}^{{II^{*} }}\).
Proof
See Online Appendix H.
Corollary 7 demonstrates that: (1) the profit of Model \(I\) is greater than that of Model \(II\) when the competitive intensity of the recycling channel is high, recycling price sensitivity is low, and the level of cost optimization factor embedded in the blockchain technology is low. Conversely, when the competitive intensity of the recycling channel is high, recycling price sensitivity is low, and the level of cost optimization factor embedded in the blockchain technology is high, the profit of Model \(I\) is less than that of Model \(II\). This is due to the fact that when the cost optimization factor of blockchain technology is at a higher level, the cost of the echelon utilizer can be effectively reduced, which leads it to set a higher transfer price or recycling price, which effectively increases the amount of SPBs recycled, and despite the higher competitive sensitivity factor of the recycling channel, the profit of the echelon utilizer in Mode \(II\) is lower than that in Mode \(I\) due to the lower sensitive factor of the recycling price; On the contrary, when the cost optimization factor of the blockchain technology is low, the cost of the echelon utilizer will increase, thus setting a lower transfer price or recycling price, resulting in a lower recycling quantity of SPBs, and when the competitive sensitivity coefficient of the recycling channel is high, even if the sensitivity coefficient of the recycling price is low, the profit of the echelon utilizer in the more competitive Mode \(II\) is greater than that of Mode \(I\). (2) When the recycling channel’s competitive intensity is lower and the price sensitivity of recycling is higher, the echelon utilizer profit of Model \(I\) is always less than that of Model \(II\). This is because although the competitive sensitivity coefficient of the recycling channel is smaller, the price sensitivity coefficient is larger, and each recycling participant is more sensitive to price changes, while the participation of echelon utilizers in recycling in Mode \(II\) is able to provide higher recycling prices and transfer prices, which attracts more SPBs to enter the recycling market, and thus the profits of echelon utilizers in Mode \(II\) are higher than those in Mode \(I\).
Corollary 8
If \(2n < m < m_{2}\) and \(F > F_{5}\), then \(\pi_{m}^{{I^{*} }} > \pi_{m}^{{II^{*} }}\); If \(2n < m < m_{2}\) and \(0 < F < F_{5}\), then \(\pi_{m}^{{I^{*} }} < \pi_{m}^{{II^{*} }}\); If \(m > m_{2}\), then \(\pi_{m}^{{I^{*} }} < \pi_{m}^{{II^{*} }}\).
Proof
See Online Appendix I.
Corollary 8 demonstrates that: (1) When the recycling channel’s competitive intensity is high, the recycling price’s sensitivity is low, and the blockchain technology’s cost optimization coefficient is low, the profit of Model \(I\) is greater than that of Model \(II\). Conversely, if the recycling channel’s competitive intensity is high, the recycling price’s sensitivity is low, and the blockchain technology’s cost optimization coefficient is high, the profit of Model \(I\) is smaller than that of Model \(II\). This is because when the cost optimization coefficient of blockchain technology is at a high level, the manufacturer’s cost can be effectively reduced, leading to the setting of a higher transfer price, and the amount of SPBs recycling will increase. Despite the high competitive sensitivity coefficient of recycling channels, the manufacturer’s profit in Mode \(II\) is smaller than that in mode \(I\) due to the low sensitive coefficient of recycling price. With a low cost optimization factor of blockchain technology, the manufacturer’s cost will be increased, which will cause it to set a lower transfer price, then the number of SPBs recycling will be reduced, and despite the high competitive sensitivity coefficient of the recycling channel, a sufficiently low sensitivity coefficient of the recycling price will lead to a larger manufacturer profit in Mode \(II\) than in Mode \(I\). (2) When the competition intensity in the recycling channel is lower and the sensitivity to recycling prices is higher, the manufacturer’s profit in Mode \(I\) is always smaller than that in Mode \(II\), regardless of the level of the cost optimization coefficient embedded in the blockchain technology. This is due to the fact that, according to Corollary 1, the manufacturer in Mode \(I\) sells power batteries at a wholesale price and in quantities equal to that in Mode \(II\). Therefore, the production cost of power batteries determines the profit size of the two models. Based on Corollary 3, the manufacturer’s price for recycling materials is higher in Model \(I\) than in Model \(II\). Therefore, the manufacturer’s marginal revenue from using recycled materials to produce power batteries in Model \(I\) is lower than in Model \(II\). Additionally, Corollary 5 states that the quantity of recycled materials in Model \(I\) is lower than in Model \(II\), resulting in lower profits for the manufacturer in Model \(I\) compared to Model \(II\).
Corollary 7 and Corollary 8 demonstrate that the manufacturer and echelon utilizer can both achieve maximum profit under the same conditions. This means that when the manufacturer earns the maximum profit, the echelon utilizer will also earn the maximum profit, resulting in a mutually beneficial outcome. This provides theoretical support for cooperation between the manufacturer and the echelon utilizer.